Рис. 8. Лишь Пифагор и непорочные девы могли слышать эту гармонию сфер.
Физики вечно осмеивали геологию как субъективный, неточный, описательный предмет, который нельзя даже сравнивать с «точными» науками. «Геологи, — насмехались они, — при первом появлении знака интеграла ищут, куда бы спрятаться». Кельвин говорил, что геология без чисел — не наука. Однако в случае самого Кельвина ярко высвечивается ахиллесова пята физики — уязвимость ее предпосылок, ничуть не лучших, чем постулаты безусловной веры. Изящные числа Кельвина дали ответы настолько же неверные, насколько они не были окончательными. И такой была судьба физики на протяжении всей истории.
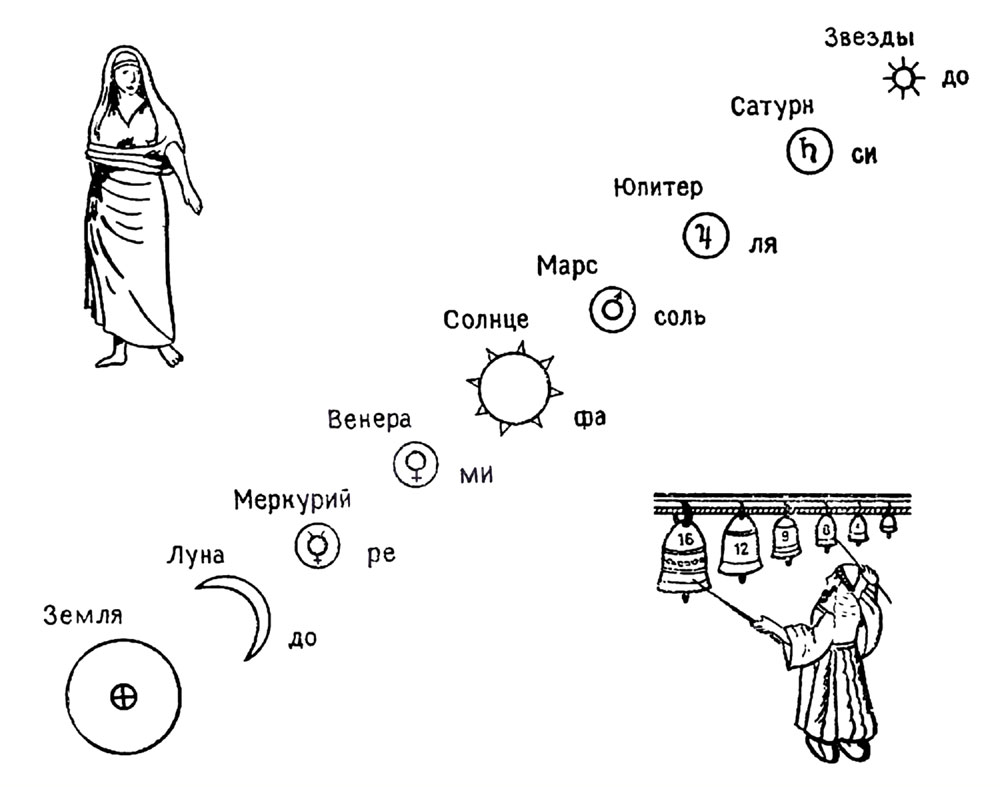
Для Пифагора и его многочисленных последователей совершенство и гармония во Вселенной не требовали доказательств. Вдохновленный музыкой ударов молотом по наковальне, Пифагор экспериментировал со струнами разной длины, с трубками, со стеклянными сосудами, наборами колоколов, чтобы найти для каждого источника звука гармонические интервалы музыкальной гаммы. Для Пифагора числа были основой всего; поэтому когда он открыл, что гармонические интервалы — это простые суммарные соотношения длин натянутых струн, его озарило, что такие же соотношения должны существовать между расстояниями до небесных тел, чтобы создать гармонию сфер — мелодию, которую могли слышать только Пифагор и непорочные девы, хотя поэты славили ее и тысячелетия спустя. Луна находилась ближе всего к Земле и имела самый низкий тон, звезды были дальше всего и издавали самые высокие звуки, а Солнце и пять известных тогда планет располагались между Землей и звездами, так что весь диапазон расстояний от Земли до звезд составлял одну октаву (рис. 8). Следовательно, относительные расстояния до всех этих небесных тел были точно определены. Наука стала точной! Говорили, что, по оценке Пифагора, один из таких небесных интервалов — расстояние до Луны — составлял 126 000 стадий (около 23 000 км, т.е. примерно одна двадцатая истинного расстояния), но нигде .не сказано, как он пришел к этому результату, поскольку сам Пифагор не оставил никаких записей. Прошло еще четыре столетия, прежде чем Гиппарх из Никеи (160—120 до н.э.) вычислил расстояние до Луны, сравнив радиус земной тени, отбрасываемой во время затмения на Луну, с радиусом Земли, который был измерен Эратосфеном (см. рис. 2). Под влиянием Пифагора гармония Вселенной стала аксиомой, в нее верили. Пифагор действительно был убежден, что слышит эту мелодию сфер. Несмотря на несостоятельность подобной идеи, гармония сфер стала общепринятой догмой на последующие 2000 лет. Шекспировские придворные говорят о ней так, что становится ясно: каждый образованный дворянин должен был непременно это знать. Но, увы, точные числа Пифагора были заблуждением.

Рис. 8. Лишь Пифагор и непорочные девы могли слышать эту гармонию сфер.
«Точные» числа архиепископа Ашера, полученные и представленные с ученостью и эрудицией, не имевшими себе равных ни до, ни после того, позволили ему установить день и час сотворения Земли; но его ответ был настолько же неверен, насколько это вообще возможно. Безупречная логика и точный расчет дают совершенную чепуху, если при этом исходят из ложной предпосылки.
Гарольд Джеффрис, самый искушенный в математике геофизик, на протяжении всей своей долгой жизни настаивал, что материки — это неподвижные тела, украшающие лик Земли, и разносил в пух и прах тех геологов, которые утверждали обратное. И не искусные операции с числами подвели его, а вера, основанная на ошибках интуиции.
Великие физики от Ньютона до Эйнштейна нисколько не сомневались в том, что первоначальный акт творения действительно имел место и именно тогда возникли все атомы Вселенной, а раньше ничего не было, хотя это и противоречит их законам сохранения вещества и энергии. Если эта предпосылка ложная, может ли какой-либо основанный на ней вывод, даже при самых лучших математических выкладках, быть признан бесспорно справедливым? Этот вопрос рассматривается в последующих главах.
Язвительное замечание Гексли о том, что самая изящная математика не позволит получить пшеничную муку из гороха, поставило общий вопрос о статусе числа в геологии. Давайте прежде всего установим внутренние различия .между разными областями знания.
Математик может быть хорошим специалистом в своей области, совсем ничего не зная о других науках. Физик может успешно работать, не зная ничего, кроме математики и физики. Но каждое действие в химии имеет корни в физике и, следовательно, в математике. Биология включает в себя сложную химию и, значит, физику и математику, вместе со своими собственными, присущими только ей переменными величинами. Геология опирается на все четыре науки.
В физике можно сформулировать проблему теоретически «ля экспериментально, изменяя только один параметр. Но сложность решения геологических задач связана с необходимостью учесть влияние столь многих факторов и в таких огромных масштабах, что невозможно изолированно рассматривать ни математические, ни физические переменные; поэтому геолог вынужден все больше и больше полагаться на опыт и качественное эклектическое суждение — утонченный синоним здравого смысла.
Многие из основных принципов физики можно экспериментально проверить в лаборатории. Но в геологии масштабы пространства и времени настолько велики, что об эксперименте речь не идет. Можно построить динамические подобные модели, но никто не может быть уверен, что не вмешаются какие-то другие факторы, которые не проявляются в масштабе возможных наблюдений, но преобладают над всеми другими факторами, если масштабы процессов или их продолжительность очень велики. Такое влияние масштаба рассматривается в ч.IV этой книги и еще раз — в последней главе.
Геологи и геофизики приближаются к истине с разных сторон. Геофизики рассматривают какой-то аспект строения Земли, создавая теоретическую математическую модель, которая ограничивает число переменных и поддающихся количественной оценке параметров. Вывод может быть справедлив для этой модели, но он будет иметь малое отношение (или вовсе никакого) к реальной Земле, хотя геофизик будет твердо в него верить, особенно если он «выдан» беспристрастным компьютером. Геолог, напротив, имеет дело с реальной Землей, видит ее без прикрас и рассуждает качественно и логично. Для геофизика опасность заключается в несовершенстве модели. Ахиллесова пята геолога — возможная неправильность его интуиции. Нельзя быть уверенным ни в том, что все относящиеся к делу законы природы уже открыты, ни в том, что не будет перейден какой-то порог, когда изменение количества создаст новое качество.
Необходимы оба подхода — и количественный, и эмпирический, и каждый из них может помочь другому прокладывать новые пути для теории и эксперимента.
Сравнимая компетентность в математике и в геологии подразумевает равноценный интеллект, но разного типа. Математика требует чистых логических рассуждений на основе установленных предпосылок. Геология отличается от большинства других наук в трех отношениях. Во-первых, как показано выше, она требует способности к эклектическому мышлению с интуитивной оценкой влияния множества переменных. Во-вторых, геология включает ретроспективный анализ причин и следствий, что наглядно проявилось в законе суперпозиции (впервые провозглашенном в 1669г. Н.Стено): последовательность слоев, их деформация и дробление, а также внедрение в них жил означают определенную историческую последовательность событий. В-третьих, геология требует способности наглядно представлять себе объекты в трех измерениях — переходить от случайных сечений в шлифах к оптическим и кристаллографическим осям кристаллизации в минерале; от выходов пород на геологической карте — к объемным структурам складок, разрывов, несогласий и интрузивных контактов; от стереоскопических аэрофотоснимков — к конфигурации глубинных структур; от отдельных пересечений буровыми скважинами — к форме рудной залежи; от случайного следа на поверхности, оставшегося от разрушенного ископаемого организма, — к мысленной реконструкции всего животного; от проекций линейности или ориентировки кливажа — к представлению о напряжениях, под действием которых они образовались; от извилистого узора множества складок — к единой картине деформаций, которую они сопровождают, и т.д.
По упомянутым выше причинам переход к количественным характеристикам в геологии начался поздно. Расстояния небесных тел от Земли, которые Пифагор выразил числами, опирались на ложную посылку. Четыре столетия спустя Эратосфен сделал гораздо более успешную попытку измерить диаметр Земли, рассуждая логически и опираясь на добротные наблюдения. Ньютон пришел к правильному заключению о сплюснутой форме Земли, что обусловлено центробежной силой, возникающей при вращении и противодействующей силе тяжести в возрастающей степени от полюсов к экватору. На этом основании Ньютон рассчитал сплюснутость Земли. Через сто лет Генри Кавендиш вычислил массу Земли; он поместил два золотых шара на концах стержня, подвешенного на нити за середину, затем измерил кручение нити, когда к одному из шаров подносили тяжелую массу. Поскольку Кавендиш знал массу притягивающихся тел, то, применив закон всемирного тяготения Ньютона для силы притяжения, измеренной по кручению нити, он смог вычислить гравитационную постоянную в законе Ньютона. Отсюда было легко подсчитать, сколько весит Земля, снова применив закон Ньютона. Но физики объявляют все эти и другие измерения параметров Земли физикой, а не геологией.
Физика с самого начала имела дело с числами. В химии количественные величины появились несколько позже, а в биологии — совсем недавно. Числовая геофизика медленно развивалась от Осмонда Фишера, лорда Кельвина и Гарольда Джеффриса до целой фаланги выдающихся современных исследователей, причем ее развитие частично совпадало со взрывом исследований в прикладной геофизике, с конца 20-х годов финансировавшейся горнодобывающей промышленностью. Двести лет назад, начиная с Ардуино, постепенно выкристаллизовалось представление о качественной относительной последовательности геологических событий, но абсолютный возраст геологических периодов был установлен лишь в этом веке. Петрология также стала количественной дисциплиной, и это постепенно распространилось на геохимию в целом. В последние два десятилетия резко расширилось применение числовых величин во всей геологии. В какой-то мере это происходило и раньше, но чрезвычайно ускорилось в результате применения мощных компьютеров, способных анализировать и обрабатывать обширные массивы разнородных данных.
Будучи неизбежными и в конечном счете нацеленными на быстрый прогресс геологии, числовые методы имеют, однако, не только положительные свойства, но и могут превратиться в слепой фетиш. Среди лабораторных работников, жонглирующих числами и оперирующих со шкалами на «черных ящиках», может появиться новое поколение исследователей, применяющих программы, роль которых они на самом деле не понимают, в постоянно суживающихся специальных областях. Они слепо верят получаемым на ЭВМ результатам и пренебрежительно относятся к методам своих более мудрых предшественников. Я наблюдал резвых мальчишек, с гордостью накапливающих множество распечаток с компьютеров — потенциально богатую руду, но не умеющих выделять из нее ценное вещество. Предостережение Гексли о внесении и получении мусора («какой мусор внесем, такой и получим») здесь даже еще более уместно. Ограничения смежных наук можно не заметить. Ловушки таятся в допущениях и в частном характере условий, включенных в математическое обеспечение.
Многочисленны ложные выводы, являющиеся следствием той или иной из этих опасностей. Я уже упоминал ошибку Кельвина, упустившего неизвестный тогда фактор. К другим примерам можно отнести неправильное применение статистики Симпсоном (гл. 8), веру Макелинни в результаты, полученные по неправильной программе (гл. 14), интерпретацию голубых сланцев с позиций не относящегося к делу эксперимента (гл. 14).
Популяции ископаемых животных, обнаруженных в конкретных местах, — ископаемые фауны — используются уже более ста лет для оценки сходства между регионами. Фаунистические соотношения свидетельствуют о миграции животных между регионами либо об изоляции этих регионов; таким образом, растущий объем данных позволяет выделить фаунистические провинции и ареалы. Они, в свою очередь, накладывают ограничения на палеогеографические реконструкции. В последние годы был проделан тщательный анализ полноты списков фауны и систематического влияния, которое вносится тем, что определяющий фауну палеонтолог работал в каком-то одном регионе. Строгие статистические методы, примененные после исключения космополитных ископаемых видов и случаев сомнительных определений, дают твердые числа для оценки сходства. Опираясь на эти методы, д-р Клайв Барретт вычислил свой «индекс провинциальности», разделив число общих для провинций родов на удвоенное число необщих родов. Преодолев должным образом трудности проведения корреляции для коротких интервалов времени и добившись действительной сравнимости сопоставляемых мест обитания, Барретт составил таблицу таких индексов и на ее основе провел обзор современных тектонических гипотез. Как и у Ашера и Кельвина, эрудиция и добросовестность Барретта безупречны; сложность заключается в предпосылках.
Дж.Г.Макин, прежде работавший в Техасском университете, писал:
«Когда механический анализ подменяет анализ мыслительный я когда число как самоцель подменяет понимание, возникает опасность..,
Самый акт измерений по жесткой схеме дает твердое ощущение, что цель достигнута. Если измерения сложны, требуют каких-то особых методов и аппаратуры и при этом используется специальный жаргон, все это дает исследователю приятное чувство принадлежности к группе избранных и преодоления рубежей. Представление результатов упрощается применением математических символов, и даже если девять из десяти заинтересованных геологов не разберутся в этих символах, автор может быть уверен, что на семерых из десяти это по крайней мере произведет впечатление. Лаконичными математическими уравнениями можно говорить о разных вещах выразительно и даже высокомерно, что можно расценивать — в зависимости от точки зрения — как преимущество или как недостаток такой записи, но эти уравнения столь бессмысленны, что, если их изложить словами, это смутило бы, вероятно, даже их автора».
Задолго до появления электронно-вычислительных машин Томас Чемберлин, основатель гарвардского издания «Journal of Geology», писал: «Очаровывающая выразительность строгого математического анализа с его атмосферой точности и изящества не должна мешать нам видеть недостатки предпосылок, которые определяют весь ход процесса. Возможно, нет более коварного и опасного обмана, чем сложный и изящный математический анализ, построенный на неосновательных предпосылках».
Должна ли в таком случае геология оставаться качественной наукой? Конечно, нет. Из-за присущего ей широкого спектра взаимозависимых переменных геология, вероятно, выиграет больше от огромной мощности ЭВМ, чем большинство других наук. Но широкое всеобщее обучение и основательный опыт в наблюдении реальных пород в поле сегодня еще более необходимы, чем раньше. Даже технические вспомогательные средства, такие, как автомобиль и вертолет, имеют свои недостатки: до их появления геологи ходили пешком от одной точки наблюдения к другой и буквально спотыкались об искомые горные породы, получая неожиданную информацию, а теперь, наоборот, главную роль играют принятые в данное время допущения.